CoRe Technology Initiative

I’ve set about updating our combat modules to include a bot that is, to be blunt, a bit of a cheater. The basis of the bot’s strategy is simple, to assume actions soon-to-be taken in advance and devise the best current course of action based on these future predictions. It is an adaptation of the minimax theorum, which I’m sure most of you have already heard of. For those in need of a refresher, however…

The minimax theorem states:

For every two-person, zero-sum conflict with finite strategies, there exists a value V and a mixed strategy for each player, such that (a) Given player 2’s strategy, the best payoff possible for player 1 is V, and (b) Given player 1’s strategy, the best payoff possible for player 2 is -V.

That is to say, for every interaction in combat, your decisions can be broken into actions in a step-wise mannerism. For every aggression against you, there is a finite set of reactions one can perform. As such, the “Minimax Bot” as I’ll call it performs a recursive computation along the following lines:

function minimax(node, depth)
    if node is a terminal node or depth = 0
        return the heuristic value of node
    else
        let α := -∞
        foreach child of node        { evaluation is identical for both players }
            let α := max(α, -minimax(child, depth-1))
        return α

In order to better understand the depth of MM-Bot one must first understand the state evaluation function. This function is a weighted summation of current advantage (or perhaps disadvantage) that looks something like the following.

function evaluation(current_state)
    advantage = 0
    for each opening in current_state.defense
        advantage = advantage - 1
    for each opportunity in current_state.attacks
        advantage = advantage + 1
    if current_state.include(struck) == true
        advantage - 10
    if current_state.include(strike) == true
        advantage + 10
    magnitude = 1
    for each flank in current_state.position
        magnitude = magnitude /2
    magnitude = magnitude * current_state.mobile_rank
    advantage = advantage * magnitude
    return advantage

That being the template version which is interfaced by just who the current_state refers to, opponent or current MM-Bot’s style configuration depending the current loop upon the minimax recurse. Now, in layman’s terms, that simply means the following. You perform an action directed at MM-Bot, which it calculates a static evaluation for using the above method notated. It now creates a sub-set of all possible reactions, and upon those reactions, recurses back to your coming reaction, and so on, and so on, essentially generating a tree of all possible actions and reactions. Now, each of these possibilities is ranked based on the evaluation function. At each step of yours, it tries to maximize, making the assumption that you will perform the “best” action in any scenario, and then attempts to minimize the evaluation function at each of its possible choices (IE: performs the “worst” action for -you-). The depth within the minimax recursion is iterativally deeping, extending its allotted amount of calculations based upon the time it guesses it has left in order to make a choice. At the end of look-aheads (say, X ‘moves’ ahead), it finds the one with the lowest possible score, and returns this value all the way up the tree of actions to see the best current-action it may take (as opposed to just choosing the ‘best’ at each step quickly without investigating possible consequences of future interaction).

This was fairly computationally heavy, and while fine in interactions with no time limit, was at first impractical on my test setups in real-time. However, I managed to rework the theorem to support alpha-beta pruning, which is less naive in the path of the tree it even bothers investigating.

function alphabeta(node, depth, α, β)
    (* β represents previous player best choice - doesn't want it if α would worsen it *)
    if node is a terminal node or depth = 0
        return the heuristic value of node
    foreach child of node
        α := max(α, -alphabeta(child, depth-1, -β, -α))
        (* use symmetry, -β becomes subsequently pruned α *)
        if β≤α
            break                             (* Beta cut-off *)
    return α

(* Initial call *)
alphabeta(origin, depth, -infinity, +infinity)




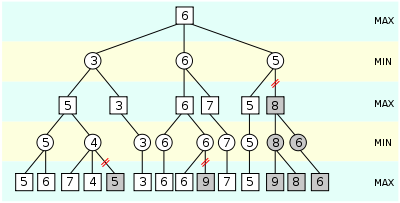
An illustration of alpha-beta pruning. The grayed-out subtrees need not
be explored (when moves are evaluated from left to right), since we
know the group of subtrees as a whole yields the value of an equivalent
subtree or worse, and as such cannot influence the final result.

This allows for a much more efficient process and allows an average look-ahead of 10 or so forth-coming actions to be computed in the average recorded Marshal Cadet reaction time of 175 milliseconds. Assuming your expertise, you might hope to shave some of that off, but the threat still remains – are you up to the challenge of an opponent who is constantly acting from the future?

I’ll be installing this momentarily after my research report is submitted back to the CoRe Technology DB, I encourage you all to help with my research in it. I’m certain I’ll be able to create far stronger simulations based off data I can gather from its performance against a wide variety of strengths and weaknesses, and I believe its fundamental properties will enforce a stronger discipline from everyone, myself included, by pointing out the weakness of rash or uneducated assumptions within the immediate flow of battle.

-Crono Arinborn

One Response to “The Recursive Look Ahead Bot”

1. Crono Says:
   March 20th, 2009 at 9:54 am

   Status update: Up and running. Upon loading simulation just needs to be updated with the interface and given a specific depth (look ahead count, this drastically alters the difficulty around the 4-5 plydepth marker).

   If you have any issues with it, please feel free to find me and I’ll try to assist as best as I can.

Leave a Reply